Синтез логических схем
 Лабораторная работа выполняется с помощью учебного лабораторного стенда LESO2.
Лабораторная работа выполняется с помощью учебного лабораторного стенда LESO2.
1 Цель работы
Научиться синтезировать логические схемы по заданной таблице истинности.
2 Краткие теоретические сведения
Любая логическая схема без памяти полностью описывается таблицей истинности. Эта таблица является исходной информацией для синтеза схемы на основе логических элементов «И», «ИЛИ», «НЕ». Для разработки требуемого цифрового устройства сначала на основе таблицы истинности записывают его логическое выражение. Затем с целью упрощения цифрового устройства минимизируют его логическое выражение и далее разрабатывают схему, реализующую полученное логическое выражение. Логические выражения можно получить двумя способами:
- на основе совершенной дизъюнктивной нормальной формы (СДНФ);
- на основе совершенной конъюнктивной нормальной формы (СКНФ).
Совершенная дизъюнктивная нормальная форма (СДНФ)
Функция представляется суммой групп. Каждая группа состоит из произведения, в которую входят все переменные.
Например:
f(x1,x2,x3) = x1·x2·x3 + x1·x2·x3 + x1·x2·x3
Совершенная конъюнктивная нормальная форма (СКНФ)
Функция представляется произведением групп. Каждая группа состоит из суммы, в которую входят все переменные.
Например:
f(x1,x2,x3) = (x1+x2+x3)·(x1+x2+x3)·(x1+x2+x3)
Если схема имеет несколько выходов, то каждый выход описывается своей функцией. Такая система функций называется системой собственных функций. СДНФ составляется на основе таблицы истинности по следующему правилу: для каждого набора переменных, при котором функция равна 1, записывается произведение, в котором с отрицанием берутся переменные, имеющие значение «0».
Пример:
Таблица 2.1 – Заданная таблица истинности
| x1 | x2 | x3 | y |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
СДНФ:
y = f(x1,x2,x3) = x1·x2·x3 + x1·x2·x3 + x1·x2·x3 + x1·x2·x3
СКНФ составляется на основе таблицы истинности по правилу: для каждого набора переменных, при котором функция равна 0, записывается сумма, в которой с отрицанием берутся переменные, имеющие значение 1.
Таблица 2.2 – Заданная таблица истинности
| x1 | x2 | x3 | y |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
СКНФ:
y = f(x1,x2,x3) = (x1+x2+x3)·(x1+x2+x3)·(x1+x2+x3)·(x1+x2+x3)
На основе полученных выражений можно составить схему устройства, реализующего заданную функцию. Схема устройства, полученная на основе СДНФ, изображена на рисунке 2.1, а на основе СКНФ на рисунке 2.2.
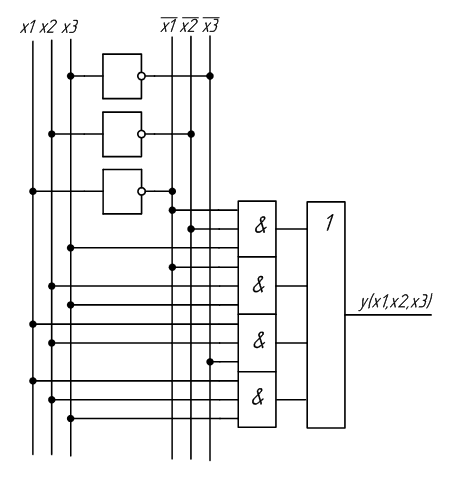
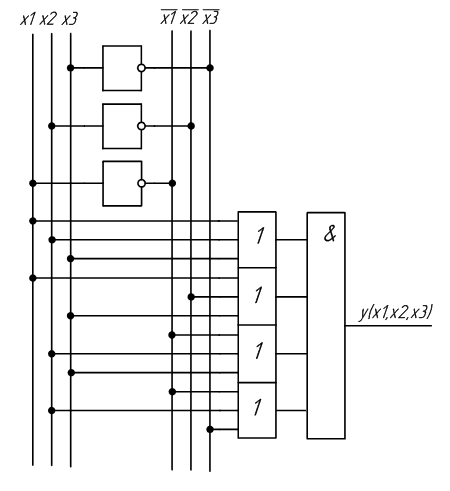
С целью упрощения цифрового устройства применяют минимизацию функций. Используя законы алгебры логики, можно упростить исходную функцию.
y(x1,x2,x3) = x1·x2·x3 + x1·x2·x3 + x1·x2·x3 + x1·x2·x3 =
= x1·x3·(x2+x2) + x1·x2·(x3+x3) = x1·x3 + x1·x2
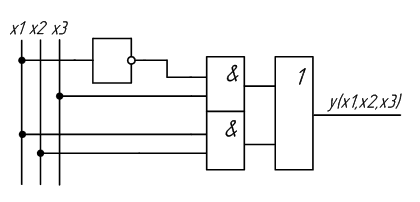
На основе полученного выражения составим новую схему устройства (рисунок 2.3).
3 Задание к работе
3.1 Исследовать схему, полученную по таблице истинности (таблица 2.1) на основе СДНФ. Для этого сконфигурировать ПЛИС в соответствии со схемой рисунок 2.1. Подключить к входам схемы переключатели S7,S8,S9, а к выходу светодиод LED 8. Схема устройства в среде Quartus II будет выглядеть в соответствии с рисунком 3.1.
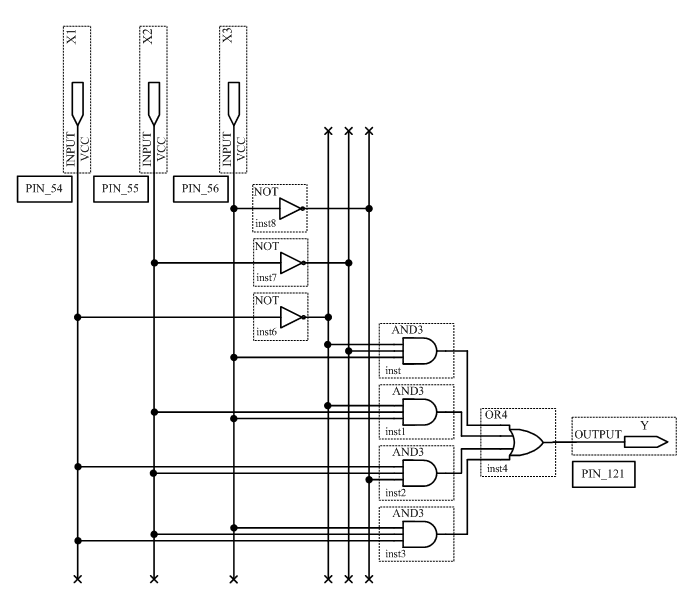
Устанавливая на входах схемы с помощью переключателей все возможные кодовые комбинации и наблюдая за светодиодом, заполнить таблицу истинности исследуемого устройства.
3.2 Исследовать схему, полученную по таблице истинности (таблица 2.2) на основе СКНФ.
Для этого сконфигурировать ПЛИС в соответствии со схемой рисунок 2.2. Подключить к входам схемы переключатели S7,S8,S9, а к выходу светодиод LED 8. Схема устройства в среде Quartus II будет выглядеть в соответствии с рисунком 3.2. Можно не создавать новый проект, а отредактировать проект, созданный в пункте 3.1. Устанавливая на входах схемы с помощью переключателей все возможные кодовые комбинации и наблюдая за светодиодом, заполнить таблицу истинности исследуемого устройства.
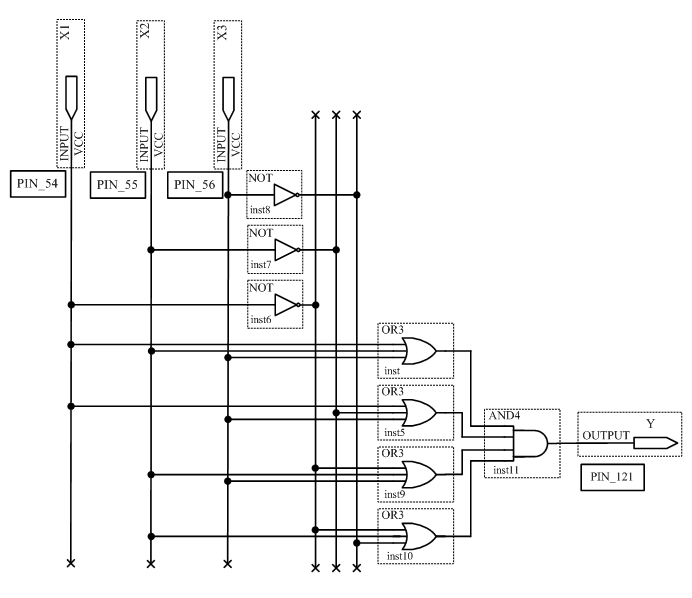
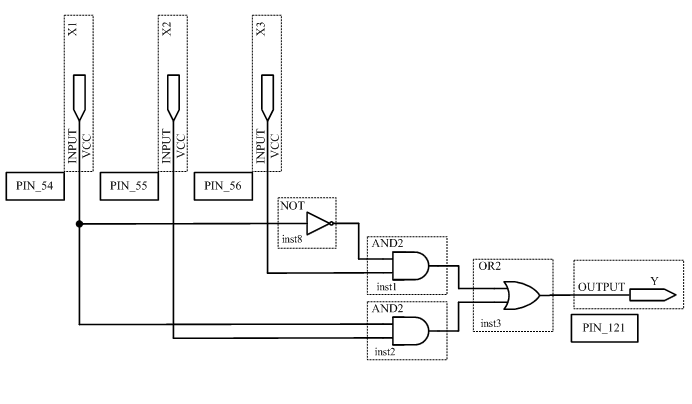
3.3 Исследовать минимизированную схему (рисунок 2.3.)
Для этого сконфигурировать ПЛИС в соответствии со схемой рисунок 2.3. Подключить к входам схемы переключатели S7,S8,S9, а к выходу светодиод LED 8. Схема устройства в среде Quartus II будет выглядеть в соответствии с рисунком 3.3. Устанавливая на входах схемы с помощью переключателей все возможные кодовые комбинации и наблюдая за светодиодом, заполнить таблицу истинности устройства.
4 Содержание отчета
- Цель работы.
- Заданная таблица истинности.
- Логическое выражение на основе СДНФ.
- Логическое выражение на основе СКНФ.
- Минимизированное логическое выражение.
- Схемы, синтезированные на основе СДНФ, СКНФ и в результате минимизации.
- Таблицы истинности, полученные в результате исследования схем.
- Выводы.
5 Контрольные вопросы
- Что такое СДНФ?
- Что такое СКНФ?
- Как записать СДНФ, используя таблицу истинности устройства?
- Как записать СКНФ, используя таблицу истинности устройства?
- Как разработать схему логического устройства, используя СДНФ?
- Как разработать схему логического устройства, используя СКНФ?
- Как лучше синтезировать логическое устройство (на основе СДНФ или СКНФ), если значение функции в таблице истинности имеет больше нулей, чем единиц?
- Как разработать логическое устройство, если оно имеет несколько выходов?
- Что такое минимизация логического выражения?
- Запишите основные законы алгебры логики.
- Расскажите, как определить таблицу истинности логического устройства экспериментально, используя лабораторный стенд.
Узнать больше об аппаратном синтезе логическ схем в ПЛИС можно из статьи
Архитектура ПЛИС. Часть 1. Логический элемент


